Las matemáticas han representado una de las dificultades más comunes en las aulas desde hace décadas. Su aprendizaje no solo ha llevado a muchos alumnos a desconectarse de ellas, sino que incluso provocan ansiedad y estrés. Actualmente, muchos centros escolares y equipos docentes apuestan por transformar las matemáticas en algo lúdico y manipulativo. Con frecuencia y con la idea de mejorar el aprendizaje de los alumnos, introducimos cambios metodológicos que hemos visto que funcionan en otros contextos.
Muchos centros escolares y equipos docentes apuestan por transformar las matemáticas en algo lúdico y manipulativo.
La idea no es errónea, pero para asegurarnos que estos cambios también van a tener un efecto positivo en nuestro contexto debemos asegurarnos de que también nuestros objetivos han cambiado.
¿Qué nos dice la neurociencia sobre el aprendizaje matemático?
La neurociencia ha aportado investigaciones recientes centradas en el aprendizaje de las habilidades numéricas básicas para el aprendizaje matemático inicial, que pueden ayudar a mejorar, disminuir o erradicar las dificultades presentes en el proceso de enseñanza-aprendizaje de las matemáticas.
Nacemos con un sentido numérico primitivo y ya desde bebés somos capaces de identificar cambios en las cantidades numéricas.
En los últimos años, las investigaciones neurocientíficas han revelado que, al nacer, nuestro cerebro no es una página en blanco, sino que nacemos con un sentido numérico primitivo y ya desde bebés somos capaces de identificar cambios en las cantidades numéricas. Diversos estudios y experimentos han demostrado que niños entre 4 y 6 años que no saben sumar, resuelven operaciones sin la necesidad de realizar cálculos exactos ni complejos. Esto viene dado que disponen de una comprensión de la aritmética, basada en la intuición.
Gracias a las evidencias neurocientíficas, sabemos que la Educación Infantil es una oportunidad para potenciar esta intuición e ir, de forma progresiva y respetuosa, desarrollando habilidades y capacidades lógico-matemáticas.
5 claves matemáticas a tener en cuenta desde una perspectiva neuroeducativa
1. Intuición matemática: de lo concreto a lo abstracto
Los estudios neurocientíficos han permitido demostrar que, de forma espontánea y natural, los más pequeños pueden resolver operaciones básicas, estimaciones y comparaciones sin haber adquirido previamente un lenguaje aritmético. De esta manera, es importante potenciar la capacidad numérica intuitiva de la que disponen. ¿Cómo podemos fomentar esta intuición?
Con el objetivo de ir desarrollando el razonamiento matemático, la comprensión y adquisición numérica es imprescindible aportar situaciones en las que los alumnos identifiquen, en situaciones de la vida cotidiana y su entorno inmediato. Por este motivo, es necesario incentivar situaciones de diálogo y reflexión en las que vayan identificando, por ejemplo, cuántas canicas hay en un conjunto; qué lápices son más cortos y cuáles más largos, incluso reconocer cuantas figuras o formas geométricas son de un color u otro.
Es imprescindible aportar situaciones en las que los alumnos identifiquen, en situaciones de la vida cotidiana y su entorno inmediato.
En EMAT, nuestro programa de matemáticas para infantil y primaria, se llevan a cabo sesiones (por ejemplo, en 3 años) en las que los alumnos potencian esta intuición proporcionando juegos y actividades que les permite desarrollar la intuición mediante situaciones contextualizadas, alejándonos de fórmulas ni cálculos demasiado complejos y potenciado un escenario de aprendizaje emocionalmente positivo, para darles la oportunidad de que vayan relacionando el cálculo a su significado.
2. La manipulación y la experimentación como base del aprendizaje matemático
Con el objetivo de potenciar la intuición innata e ir desarrollando la comprensión numérica es necesario que la manipulación y la experimentación sean protagonistas durante el proceso de aprendizaje matemático. Por ello, es clave fomentar momentos y experiencias en las que los alumnos puedan observar e interactuar en el entorno y experimentar de forma tangible los objetos que los ayudan a ir adquiriendo estrategias y herramientas para pasar del pensamiento concreto al abstracto.
EMAT ofrece una secuenciación de las sesiones y los aspectos matemáticos teniendo en cuenta la importancia de la manipulación y experimentación de estos.
EMAT ofrece una secuenciación de las sesiones y los aspectos matemáticos teniendo en cuenta la importancia de la manipulación y experimentación de estos. Por ejemplo, en una sesión de 3 años los alumnos exploran la medida con objetos, proporcionándoles soportes visuales y físicos que les ayuden a realizar representaciones numéricas y conseguir, de forma progresiva y respetuosa con diversos ritmos de aprendizaje, una comprensión abstracta de los conceptos presentados.
3. La curiosidad, la sorpresa y el juego como herramientas de aprendizaje matemático.
Tal como afirma Francisco Mora, doctor en Medicina y Neurociencia, «la forma más directa de despertar la atención y el interés, mecanismo imprescindible para el aprendizaje, es suscitar la curiosidad y la sorpresa». La neuroeducación demuestra que la sorpresa es uno de los aspectos más importantes para captar la atención de los alumnos. Cuando algo nos sorprende, el tálamo, que es el centro de la atención, se activa con rapidez De esta manera, dado que la sorpresa activa la atención, es fundamental para que el aprendizaje sea significativo.
La sorpresa es uno de los aspectos más importantes para captar la atención de los alumnos.
Junto a la sorpresa y la curiosidad, el juego es otro de los ingredientes esenciales en el proceso de enseñanza y aprendizaje por sus múltiples beneficios de su uso en el contexto educativo a nivel socioemocional y cognitivo. El juego permite la liberación de dopamina en los circuitos cerebrales del sistema de recompensa del cerebro, lo que potencia la implicación y la participación de los alumnos para continuar aprendiendo.
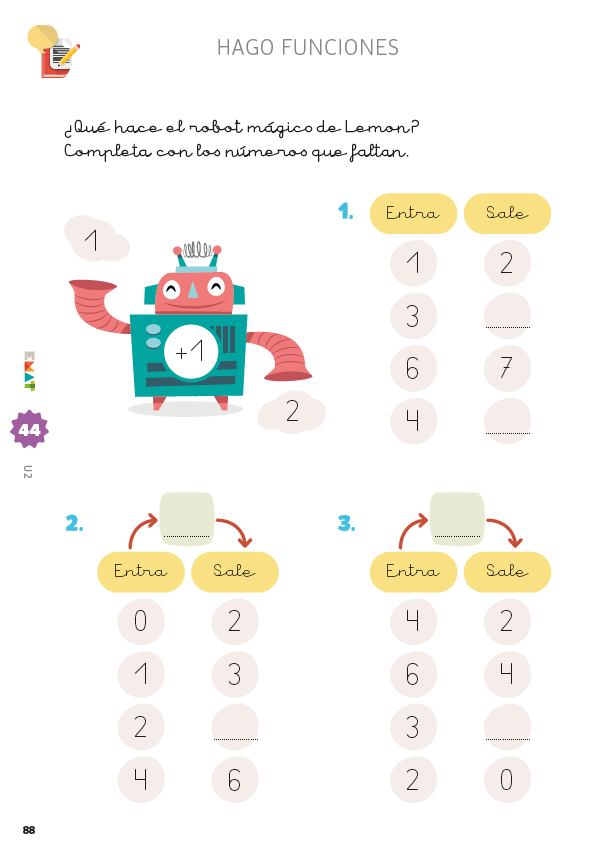
En EMAT, a través del juego y la sorpresa durante el proceso de aprendizaje, los alumnos pueden conocer y adquirir conceptos que de entrada pueden resultar abstractos y complejos. En Infantil, como puedes ver en el ejemplo de arriba, la máquina es una actividad para operar cantidades y practicar las operaciones simples y las series; y permitimos desarrollar un concepto intuitivo de la función trabajando con el robot de nombres mágicos.
En nuestra clase ha aparecido la Máquina Mágica de doña Manolita @tekmanBooks pic.twitter.com/2q0cwJqaGJ
— Ceip Ángel Esteban (@ceipangelsteban) November 16, 2015
4. Pensamiento divergente y creatividad
Las matemáticas han estado durante décadas asociadas a solucionar problemas y operaciones mediante algoritmos y soluciones exactas, únicas y complejas. Pero bien sabemos que, gracias a estas, estos inventos o construcciones han sido posibles gracias a mentes creativas que previamente han reflexionado sobre un tema, han explorado y propuesto las múltiples maneras de llegar a una solución, las han llevado a la práctica, han errado y finalmente, después de un largo proceso, han encontrado la mejor solución al problema o tema propuesto.
Es importante dar a los alumnos la oportunidad de desarrollar su pensamiento creativo y crítico.
Por ello, es importante dar a los alumnos la oportunidad de desarrollar su pensamiento creativo y crítico ante una situación y experiencia con el objetivo no tan solo de encontrar una solución a un problema, sino de cuestionar asunciones, superar límites y descubrir patrones o atributos que a simple vista no se identifican.
Por ejemplo, en el hecho de permitirles libremente clasificar un conjunto de botones, se fomenta la creatividad del alumnado al tener que observar y manipular analíticamente los objetos, identificar las diversas formas de clasificación (ya sea por su forma, su tamaño, su color, su rugosidad, etc) y decidir qué criterio van a escoger para llevar a cabo la clasificación.
5. La diversidad en el aula, una oportunidad matemática
Nuestro objetivo es ofrecer múltiples soportes y recursos, incorporando los beneficios de las diferentes formas de aprender de la cultura de pensamiento o del aprendizaje cooperativo, para que el proceso de aprendizaje de las matemáticas dé respuesta a los diferentes ritmos y niveles madurativos de los alumnos.
En EMAT, por ejemplo, el diseño de las actividades ha estado pensado para que los alumnos puedan participar, potenciando sus fortalezas y practicando con aquellos contenidos y conceptos matemáticos que necesitan reforzar a través de diversas perspectivas: actividades manipulativas, canciones, juegos de mesa, juegos corporales, lecturas y cuentos, CiberEMAT (aprendizaje digital y adaptativo de las matemáticas) y mucho más. ¿Te unes a la transformación EMAT?















